--------------------------------------------------------------------------------------------------------------------
EXERCICÍOS
A seguir confira os exercícios sobre distância entre dois pontos, recomendamos que você acesse a aula sobre o assunto em Aula sobre distância entre dois pontos.
1) Calcule a distância entre os pontos A(-2,3) e B(1,5).
2) (UFRGS) Se um ponto P do eixo das abscissas é equidistante dos pontos A(1,4) e B( -6,3), a abscissa de P vale:
a) -2
b) -1
c) 0
d) 1
e) 3
3) (UFRGS) A distancia entre os pontos A( -2,y) e B(6,7) é 10. O valor de y é
a) -1
b) 0
c) 1 ou 13
d) -1 ou 10
e) 2 ou 12
4) (UFSC) Um ponto material móvel ) desloca-se no plano cartesiano e suas coordenadas variam em função do tempo t (t ≥0). A distância percorrida pelo ponto material móvel entre o ponto A para t = 0 e o ponto B para t = 6, é:
desloca-se no plano cartesiano e suas coordenadas variam em função do tempo t (t ≥0). A distância percorrida pelo ponto material móvel entre o ponto A para t = 0 e o ponto B para t = 6, é:
----------------------------------------------------------------------------------------------------------------------------------------
Distância entre dois pontos
A base da geometria analítica encontra-se na distância entre dois pontos, pois muitos conceitos são inerentes a esse. Portanto, compreender a expressão algébrica para o cálculo da distância entre dois pontos colabora para uma compreensão fidedigna de outros conceitos da geometria analítica.

Distância entre dois Pontos
A distância permeia todos os conceitos da geometria analítica, pois nesta área da matemática temos a relação de elementos geométricos com os algébricos, e o elemento básico da geometria é o ponto.
Um dos conceitos básicos que vimos na geometria é que a menor distância entre dois pontos é dada por uma reta, contudo, na geometria analítica esses pontos recebem coordenadas no plano cartesiano e por meio dessas coordenadas podemos encontrar o valor da distância entre dois pontos.
Vamos representar dois pontos quaisquer no plano cartesiano.
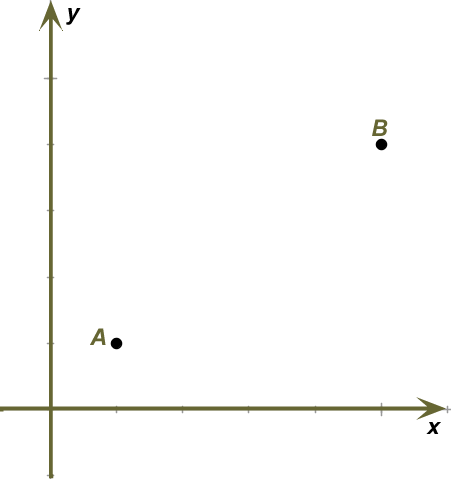
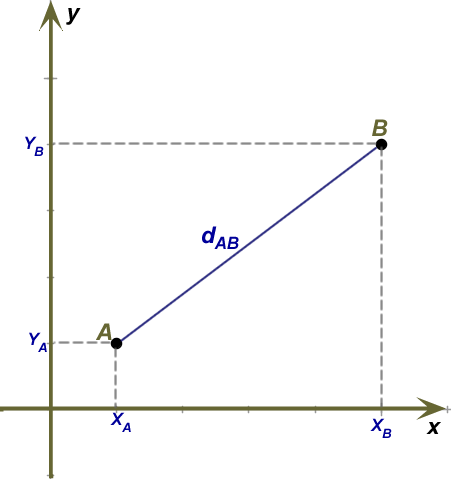
Portanto, teremos que a distância entre os pontos A e B será a medida do segmento que tem os dois pontos como extremidade. Por se tratar de dois pontos quaisquer, representaremos as coordenadas desses pontos de maneira genérica.
Sabe-se que os eixos coordenados do plano cartesiano são ortogonais, portanto, podemos construir um triângulo retângulo utilizando os pontos A e B, como mostra a figura a seguir.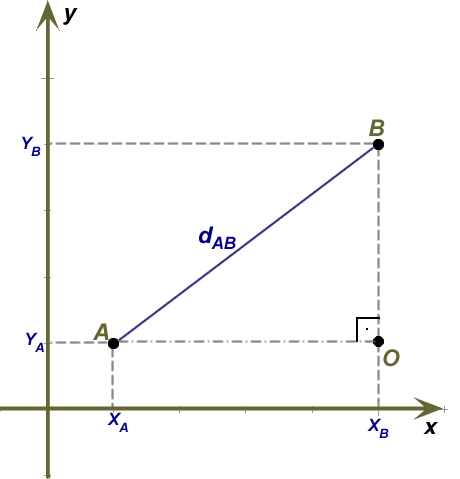

Note que o segmento AB é a hipotenusa do triângulo AOB, e a medida de AB corresponde à distância entre esses dois pontos. Por se tratar de um triângulo retângulo, podemos aplicar o teorema de Pitágoras, no qual teremos:
.png)
Note que basta fazer as diferenças das coordenadas de cada um dos pontos e elevar ao quadrado, contudo são coordenadas do eixo X com coordenadas do eixo X e de forma análoga para as coordenadas do eixo Y.
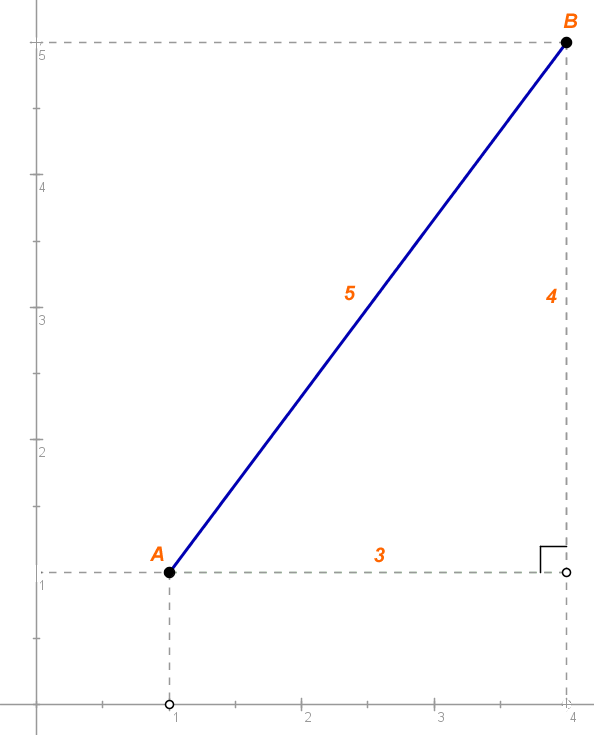
Calcule a distância entre os pontos: A (4,5) e B(1,1) e represente-os geometricamente.
Como vimos anteriormente, basta aplicar a expressão para o cálculo da distância entre dois pontos. Sendo assim:
.png)
Geometricamente:
--------------------------------------------------------------------------------------------------------------------------------------
3 ano - Lista de exercícios
Ponto Médio de um segmento e Baricentro de um Triângulo
1 – Determine o Ponto Médio do segmento de extremidades:
a) A (2, 3) e B (8, 5) b) C (3, -2) e D (-1, -6)
c) E(-2, -4) e F (5, 2) d) H (0, 7) e I (6, 0)
e) J (3, 2) e K (5, 4) f) P (-3, -4) e Q (-7, 0)
2 – Dados os pontos A (5, -2), B (3, 0), C (1 , -5) e D (-8, -1), determine as coordenadas dos pontos médios dos segmentos:
a) AB b) AD c) BD d) AC e) CD
3 – Calcule os pontos médios dos lados de um triângulo com vértices:
a) Δ ABC: A (4, 0), B (0, 6) e C(8, 2)
b) Δ EFG: E (2, -6), F(-4, 2) e G(0, 4)
c) Δ JKL: J(-3, 6), K(1, -2) e L(5, 2)
4 – Represente no plano cartesiano os triângulos XYZ e PQR. Determine as coordenadas dos pontos médios de cada lado, trace as medianas e calcule o comprimento de cada mediana.
a) Δ XYZ : X (3, 5), Y (5, 9) e Z (3, 7)
b) Δ PQR: P(2, 8), Q(2, 2) e R(6, 2)
5 – Determine as coordenadas do Baricentro (G) dos triângulos com vértices:
a) Δ ABC: A(2, 3), B(5, -1) e C(-1, 4)
b) Δ DEF: D(-1, 0), E(2, -3) e F(2, 3)
c) Δ HIJ: H(-1, -4), I(7, 6) e J(6, 1)
d) Δ KLM: K(-2, 5), L(3, 2) e M(5, -7)
6 – Uma das extremidades de um segmento é o ponto A (-2, -2). Sabendo que M (3, -2) é o ponto médios desse segmento, calcule as coordenadas do ponto B (x, y).
7 - Determine as coordenadas do ponto B sabendo que M (-1, -1) é o ponto médio de AB com A (-1, 1).
8 – O ponto A (-4, 3) é um dos extremos de um segmento cujo ponto médio é M (-1, -3). Quais são as coordenadas do outro extremo desse segmento B (x, y).
9 – Sabendo que os pontos A (x, y), B (-3, 2) e M (3, 5) são colineares, e M é o ponto médio deAB, determine as coordenadas do ponto A.
10 – Sabendo que B (4, 3) é o ponto médio de AC, tal que A esta sobre o eixo das abscissas A (x, 0) e C sobre o eixo das ordenadas C (0, y). Determine as coordenadas de A e C
11 – Calcule o perímetro do triângulo formado pelos pontos médios dos lados do triângulo de vértice A(-4, 3), B(4,-3) e C (4, 3). Represente no plano cartesiano
13 – Determine os valores de x e y sabendo que A (2, 4), B(x, 5) e C (5, y) são vértices de um Triângulo cujo baricentro é o ponto G(2, 3).
14 – Sabendo que A(x, y), B (-1, 8) e C (3, -10) são vértices de um triângulo cujo baricentro é o ponto
G (3, -2). Determine as coordenadas do vértice A.
VOCE LEMBRA: SISTEMA LINEAR
1- Resolva os sistemas abaixo:
PROBLEMAS DE APLICAÇÃO
1 – Em certo trecho em linha reta de uma estrada será instalado uma placa equidistante das extremidades. Determine a coordenada do ponto M em que a placa será instalada e a distancia dos pontos A e B em Km
2 – No esquema está representada parte de uma rua cujos extremos são árvores, serão plantadas outras duas árvores nos pontos C e D, de maneira que a distância entre uma árvore e outra seja a mesma. Conforme imagem abaixo.
(para as questões 1 e 2)
a) No esquema cada unidade corresponde a 2 m. Qual é a distância aproximada entre as árvores A e B? E entre C e D?
b) Determine as coordenadas dos pontos C e D.
 3 – (UNIRIO) Uma universidade organizou uma expedição ao sítio arqueológico de Itaboraí, um dos mais importantes do Rio de Janeiro. Para facilitar a localização dos locais de escavação, foi adotado um sistema cartesiano de coordenadas. O objetivo da expedição é realizar escavações nos pontos A (0, 0),B (6, 18) e C (18, 6). Se o chefe da expedição pretende acampar em um ponto equidistante dos locais de escavação determine as coordenadas do local do acampamento.
3 – (UNIRIO) Uma universidade organizou uma expedição ao sítio arqueológico de Itaboraí, um dos mais importantes do Rio de Janeiro. Para facilitar a localização dos locais de escavação, foi adotado um sistema cartesiano de coordenadas. O objetivo da expedição é realizar escavações nos pontos A (0, 0),B (6, 18) e C (18, 6). Se o chefe da expedição pretende acampar em um ponto equidistante dos locais de escavação determine as coordenadas do local do acampamento.
---------------------------------------------------------------------------------------------------------------------------------------
BARICENTRO DE UM TRIÂNGULO DE TRÊS PONTOS.
O triângulo é uma figura geométrica muito importante, bastante utilizado na construção civil. No estudo analítico dos triângulos, quando conhecemos as coordenadas dos seus vértices, conseguimos determinar qual é o tipo de triângulo, qual a sua área e quais as coordenadas de seu baricentro. Faremos o estudo de como obter as coordenadas do baricentro do triângulo. Antes, precisamos definir o que é baricentro.
Considere o triângulo de vértices A, B e C abaixo. Os pontos M, N e P são os pontos médios dos lados AB, BC e AC, respectivamente. Os segmentos de reta MC, AN e PB são as medianas do triângulo. Denominamos baricentro (G) de um triângulo o ponto de encontro das medianas.
Considere o triângulo de vértices A, B e C abaixo. Os pontos M, N e P são os pontos médios dos lados AB, BC e AC, respectivamente. Os segmentos de reta MC, AN e PB são as medianas do triângulo. Denominamos baricentro (G) de um triângulo o ponto de encontro das medianas.
Agora vamos considerar um triângulo no plano cartesiano de vértices A(xA, yA), B(xB, yB) e C(xC, yC) e baricentro G(xG, yG).
As coordenadas do baricentro do triângulo ABC serão dadas por:

Exemplo 1. Determine as coordenadas do baricentro do triângulo de vértices A(2, 7), B(5, 3) e C(2, 2).
Solução: Vamos calcular as coordenadas do Baricentro do triângulo separadamente, para não haver confusão no entendimento da fórmula, que é muito simples.
Sabemos que:
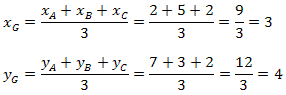
Portanto, o baricentro do triângulo ABC tem coordenadas G(3, 4).
Exemplo 2. Determine as coordenadas do vértice B do triângulo ABC sabendo que seu baricentro tem coordenadas G(5, 8) e que os outros dois vértices são A(5, 8) e C(7, 6).
Solução: Como conhecemos as coordenadas do baricentro do triângulo e as coordenadas de dois vértices, vamos utilizar a fórmula para a determinação do baricentro para determinar as coordenadas de B.
Segue que:
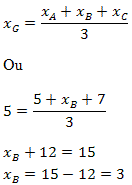
Temos também que:

Portanto, o vértice B tem coordenadas B(3,1O)

Exemplo 1. Determine as coordenadas do baricentro do triângulo de vértices A(2, 7), B(5, 3) e C(2, 2).
Solução: Vamos calcular as coordenadas do Baricentro do triângulo separadamente, para não haver confusão no entendimento da fórmula, que é muito simples.
Sabemos que:
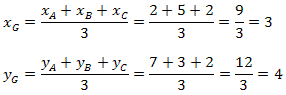
Portanto, o baricentro do triângulo ABC tem coordenadas G(3, 4).
Exemplo 2. Determine as coordenadas do vértice B do triângulo ABC sabendo que seu baricentro tem coordenadas G(5, 8) e que os outros dois vértices são A(5, 8) e C(7, 6).
Solução: Como conhecemos as coordenadas do baricentro do triângulo e as coordenadas de dois vértices, vamos utilizar a fórmula para a determinação do baricentro para determinar as coordenadas de B.
Segue que:
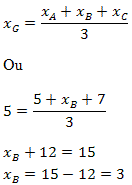
Temos também que:

Portanto, o vértice B tem coordenadas B(3,1O)
----------------------------------------------------------------------------------------------------------------------------------------
PONTO MÉDIO DE UM SEGMENTO.
segmento de reta possui inúmeros pontos alinhados, mas somente um deles irá dividir o segmento em duas partes iguais. A identificação e a determinação do ponto médio de um segmento de reta será demonstrado com base na ilustração a seguir.
.jpg)
O segmento de reta AB terá um ponto médio (M) com as seguintes coordenadas (xM, yM). Observe que os triângulos AMN e ABP são semelhantes, possuindo os três ângulos respectivamente iguais. Dessa forma, podemos aplicar a seguinte relação entre os segmentos que formam os triângulos. Veja:
.jpg)
Podemos concluir que AB = 2 * (AM), considerando que M é o ponto médio do segmento AB. Temos:
.jpg)
xP – xA = 2*(xM – xA)
xB – xA = 2*(xM – xA)
xB – xA = 2xM – 2xA
2xM = xB – xA + 2xA
2xM = xA + xB
xM = (xA + xB)/2
Utilizando método análogo, conseguimos demonstrar que yM = (yA + yB )/2.
Portanto, considerando M o ponto médio do segmento AB, temos a seguinte expressão matemática capaz de determinar a coordenada do ponto médio de qualquer segmento no plano cartesiano:
xB – xA = 2*(xM – xA)
xB – xA = 2xM – 2xA
2xM = xB – xA + 2xA
2xM = xA + xB
xM = (xA + xB)/2
Utilizando método análogo, conseguimos demonstrar que yM = (yA + yB )/2.
Portanto, considerando M o ponto médio do segmento AB, temos a seguinte expressão matemática capaz de determinar a coordenada do ponto médio de qualquer segmento no plano cartesiano:
.jpg)
Percebemos que o cálculo da abscissa xM é a média aritmética entre as abscissas dos pontos A e B. Assim, o cálculo da ordenada yM é a média aritmética entre as ordenadas dos pontos A e B.
Exemplo 1
Dadas as coordenadas dos pontos A(4,6) e B(8,10) pertencentes ao segmento AB, determine as coordenadas do ponto médio desse segmento.
xA = 4
yA = 6
xB = 8
yB = 10
xM = (xA + xB) / 2
xM = (4 + 8) / 2
xM = 12/2
xM = 6
yM = (yA + yB) / 2
yM = (6 + 10) / 2
yM = 16 / 2
yM = 8
As coordenadas do ponto médio do segmento AB é xM (6, 8).
Exemplo 2
Dados os pontos P(5,1) e Q(–2,–9), determine as coordenadas do ponto médio do segmento PQ.
xM = [5 + (–2)] / 2
xM = (5 – 2) / 2
xM = 3/2
yM = [1 + (–9)] / 2
yM = (1 – 9) / 2
yM = –8/2
yM = –4
Portanto, M(3/2, –4) é o ponto médio do segmento PQ.
Exemplo 1
Dadas as coordenadas dos pontos A(4,6) e B(8,10) pertencentes ao segmento AB, determine as coordenadas do ponto médio desse segmento.
xA = 4
yA = 6
xB = 8
yB = 10
xM = (xA + xB) / 2
xM = (4 + 8) / 2
xM = 12/2
xM = 6
yM = (yA + yB) / 2
yM = (6 + 10) / 2
yM = 16 / 2
yM = 8
As coordenadas do ponto médio do segmento AB é xM (6, 8).
Exemplo 2
Dados os pontos P(5,1) e Q(–2,–9), determine as coordenadas do ponto médio do segmento PQ.
xM = [5 + (–2)] / 2
xM = (5 – 2) / 2
xM = 3/2
yM = [1 + (–9)] / 2
yM = (1 – 9) / 2
yM = –8/2
yM = –4
Portanto, M(3/2, –4) é o ponto médio do segmento PQ.


Muito bom !
ResponderExcluirexercicio para pratica muito bom.tá ajudando.
ResponderExcluirtem o gabarito ?
ResponderExcluirFico muito agradecido em ver uma das minhas lista de exercícios sendo utilizada e meu blog sendo citado e divulgado na fonte. Valeu.! Professor Gleidston Gomes (cedt-matematica.blogspot.com.br)
ResponderExcluirEste comentário foi removido pelo autor.
ResponderExcluirEste comentário foi removido pelo autor.
ExcluirEste comentário foi removido pelo autor.
ResponderExcluirOnde encontro as respostas?
ResponderExcluirOnde encontro as respostas?
ResponderExcluirOnde encontro as respostas?
ResponderExcluirpqp
ResponderExcluirOnde encontro a respostas
ResponderExcluirOnde encontro a respostas
ResponderExcluirexcelente, continue com esse trabalho maravilhoso, ajuda bastante a quem está precisando.
ResponderExcluirAlguém pode mim ajudar
ResponderExcluirNo triângulo de vértices A(3,6),B(5,9) e C(4,7); determine as coordenadas do ponto médio de cada lado e as coordenadas do barricentro?
Ameeeei! Muito completo e excelente para treinar.
ResponderExcluir